假设对于函数 f f f
lim x → c f ( x ) = L \displaystyle \lim _{x\to c} f(x)=L x → c lim f ( x ) = L
即:只要 x x x c c c f ( x ) f(x) f ( x ) L L L
用 ε − δ \varepsilon -\delta ε − δ
∀ ε > 0 , ∃ δ > 0 , s . t . 0 < ∣ x − c ∣ < δ ⟹ ∣ f ( x ) − L ∣ < ε \displaystyle \forall \varepsilon >0,\ \exists \delta >0,\ s.t.\ 0<|x−c|< \delta \Longrightarrow |f(x)-L|< \varepsilon ∀ ε > 0 , ∃ δ > 0 , s . t . 0 < ∣ x − c ∣ < δ ⟹ ∣ f ( x ) − L ∣ < ε 说白了就是:无论给定任何一个数字 ε ( ε > 0 ) \varepsilon (\varepsilon >0) ε ( ε > 0 ) δ ( δ > 0 ) \delta ( \delta >0) δ ( δ > 0 ) x x x c c c δ \delta δ f ( x ) f(x) f ( x ) L L L ε \varepsilon ε
例:已知 f ( x ) = { 2 x x ≠ 5 x x = 5 , f( x) =\begin{cases} 2x & x\neq 5\\ x & x=5 \end{cases}, f ( x ) = { 2 x x x = 5 x = 5 , lim x → 5 f ( x ) = 10 \displaystyle \lim _{x\rightarrow 5} f( x) =10 x → 5 lim f ( x ) = 10
根据定义,给定任意 ε ( ε > 0 ) \varepsilon (\varepsilon >0) ε ( ε > 0 ) δ ( δ > 0 ) \delta ( \delta >0) δ ( δ > 0 ) δ = f u n c t i o n o f ε \delta =function\ of\ \varepsilon δ = f u n c t i o n o f ε
P r o o f . \mathnormal{Proof.} P roo f .
∣ x − 5 ∣ < δ ⟹ ∣ 2 x − 10 ∣ < ε ∣ 2 x − 10 ∣ < 2 δ 2 δ = ε ⇒ δ = ε 2 ∣ 2 x − 10 ∣ < ε ∀ ε > 0 , ∃ δ > 0 , s . t . ∣ x − 5 ∣ < δ ⟹ ∣ 2 x − 10 ∣ < ε Q . E . D . \begin{aligned} & |x-5| < \delta \Longrightarrow |2x-10|< \varepsilon \\ & |2x-10| < 2\delta \\ & 2\delta =\varepsilon \Rightarrow \delta =\frac{\varepsilon }{2}\\ & |2x-10| < \varepsilon \\ & \forall \varepsilon >0,\ \exists \delta >0 ,\ s.t.\ |x-5|< \delta \Longrightarrow |2x-10|< \varepsilon \ \quad Q.E.D. \end{aligned} ∣ x − 5∣ < δ ⟹ ∣2 x − 10∣ < ε ∣2 x − 10∣ < 2 δ 2 δ = ε ⇒ δ = 2 ε ∣2 x − 10∣ < ε ∀ ε > 0 , ∃ δ > 0 , s . t . ∣ x − 5∣ < δ ⟹ ∣2 x − 10∣ < ε Q . E . D . 设 I I I c c c f , g , h f, g, h f , g , h I I I I I I c c c x x x
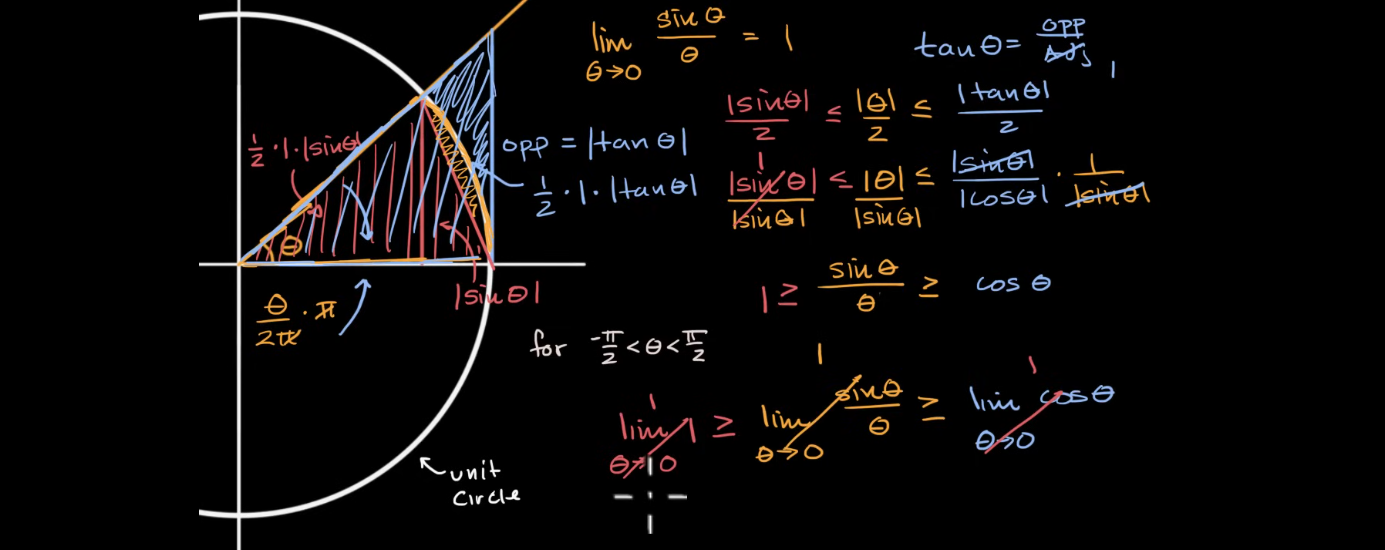
g ( x ) ⩽ f ( x ) ⩽ h ( x ) g( x) \leqslant f( x) \leqslant h( x) g ( x ) ⩽ f ( x ) ⩽ h ( x ) lim x → c g ( x ) = lim x → c h ( x ) = L \displaystyle \lim _{x\rightarrow c} g( x) =\lim _{x\rightarrow c} h( x) =L x → c lim g ( x ) = x → c lim h ( x ) = L 则,lim x → c f ( x ) = L \displaystyle \lim _{x\rightarrow c} f( x) =L x → c lim f ( x ) = L
g ( x ) g(x) g ( x ) h ( x ) h(x) h ( x ) f ( x ) f(x) f ( x )
P r o o f . \mathnormal{Proof.} P roo f .
lim θ → 0 1 − cos θ θ = lim θ → 0 ( 1 − cos θ ) ( 1 + cos θ ) θ ( 1 + cos θ ) = lim θ → 0 sin 2 θ θ ( 1 + cos θ ) = lim θ → 0 sin θ θ ⋅ lim θ → 0 sin θ 1 + cos θ = 1 ⋅ 0 = 0 Q . E . D . \begin{aligned} \lim _{\theta \rightarrow 0}\frac{1-\cos \theta }{\theta } & =\lim _{\theta \rightarrow 0}\frac{( 1-\cos \theta )( 1+\cos \theta )}{\theta ( 1+\cos \theta )}\\ & =\lim _{\theta \rightarrow 0}\frac{\sin^{2} \theta }{\theta ( 1+\cos \theta )}\\ & =\lim _{\theta \rightarrow 0}\frac{\sin \theta }{\theta } \cdot \lim _{\theta \rightarrow 0}\frac{\sin \theta }{1+\cos \theta }\\ & =1\cdot 0\\ & =0 & Q.E.D. \end{aligned} θ → 0 lim θ 1 − cos θ = θ → 0 lim θ ( 1 + cos θ ) ( 1 − cos θ ) ( 1 + cos θ ) = θ → 0 lim θ ( 1 + cos θ ) sin 2 θ = θ → 0 lim θ sin θ ⋅ θ → 0 lim 1 + cos θ sin θ = 1 ⋅ 0 = 0 Q . E . D . 函数在某一点处连续:f i s c o n t i n u o u s a t x = c ⟺ lim x → c f ( x ) = f ( c ) \displaystyle f\ is\ continuous\ at\ x=c\Longleftrightarrow \lim _{x\rightarrow c} f( x) =f( c) f i s co n t in u o u s a t x = c ⟺ x → c lim f ( x ) = f ( c )
函数在开区间连续:f i s c o n t i n u o u s o v e r ( a , b ) ⟺ f i s c o n t i n u o u s o v e r e v e r y p o i n t i n t h e i n t e r v a l f\ is\ continuous\ over\ ( a,\ b) \Longleftrightarrow f\ is\ continuous\ over\ every\ point\ in\ the\ interval f i s co n t in u o u s o v er ( a , b ) ⟺ f i s co n t in u o u s o v er e v ery p o in t in t h e in t er v a l
函数在闭区间连续:f i s c o n t i n u o u s o v e r [ a , b ] ⟺ f i s c o n t i n u o u s o v e r ( a , b ) a n d lim x → a + f ( x ) = f ( a ) , lim x → b − f ( x ) = f ( b ) \displaystyle f\ is\ continuous\ over\ [ a,\ b] \Longleftrightarrow f\ is\ continuous\ over\ ( a,\ b) \ and\ \lim _{x\rightarrow a^{+}} f( x) =f( a) ,\ \lim _{x\rightarrow b^{-}} f( x) =f( b) f i s co n t in u o u s o v er [ a , b ] ⟺ f i s co n t in u o u s o v er ( a , b ) an d x → a + lim f ( x ) = f ( a ) , x → b − lim f ( x ) = f ( b )
S u p p o s e f i s a c o n t i n u o u s f u n c t i o n a t e v e r y p o i n t o f t h e i n t e r v a l [ a , b ] Suppose\ f\ is\ a\ continuous\ function\ at\ every\ point\ of\ the\ interval\ [ a,\ b] S u pp ose f i s a co n t in u o u s f u n c t i o n a t e v ery p o in t o f t h e in t er v a l [ a , b ]
f w i l l t a k e o n e v e r y v a l u e b e t w e e n f ( a ) a n d f ( b ) o v e r t h e i n t e r v a l f\ will\ take\ on\ every\ value\ between\ f( a) \ and\ f( b) \ over\ the\ interval f w i ll t ak e o n e v ery v a l u e b e tw ee n f ( a ) an d f ( b ) o v er t h e in t er v a l F o r a n y L b e t w e e n t h e v a l u e s f ( a ) a n d f ( b ) , t h e r e e x i s t s a n u m b e r c i n [ a , b ] f o r w h i c h f ( c ) = L For\ any\ L\ between\ the\ values\ f( a) \ and\ f( b) ,\ there\ exists\ a\ number\ c\ in\ [ a,\ b] \ for\ which\ f( c) =L F or an y L b e tw ee n t h e v a l u es f ( a ) an d f ( b ) , t h ere e x i s t s a n u mb er c in [ a , b ] f or w hi c h f ( c ) = L 怎么会有这么简单的定理…
Lagrange's notation: f ′ \displaystyle f^{\prime } f ′
Leibniz's notation: d y d x \displaystyle \frac{dy}{dx} d x d y
Newton's notation: y ˙ \displaystyle \dot{y} y ˙
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h \displaystyle f^{\prime }( x) =\lim _{h\rightarrow 0}\frac{f( x+h) -f( x)}{h} f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x )
f ′ ( c ) = lim x → c f ( x ) − f ( c ) x − c \displaystyle f^{\prime }( c) =\lim _{x\rightarrow c}\frac{f( x) -f( c)}{x-c} f ′ ( c ) = x → c lim x − c f ( x ) − f ( c )
f i s d i f f e r e n t i a b i l i t y a t x = c ⟹ f i s c o n t i n u o u s a t x = c f i s n o t c o n t i n u o u s a t x = c ⟹ f i s n o t d i f f e r e n t i a b i l i t y a t x = c f\ is\ differentiability\ at\ x=c\Longrightarrow f\ is\ continuous\ at\ x=c \\ f\ is\ not\ continuous\ at\ x=c\Longrightarrow f\ is\ not\ differentiability\ at\ x=c f i s d i ff ere n t iabi l i t y a t x = c ⟹ f i s co n t in u o u s a t x = c f i s n o t co n t in u o u s a t x = c ⟹ f i s n o t d i ff ere n t iabi l i t y a t x = c
不可微的三种情况:{ 1. n o t c o n t i n u o u s 2. v e r t i c a l t a n g e t 3. s h a r p t u r n \begin{cases} 1.\ not\ continuous\\ 2.\ vertical\ tanget\\ 3.\ sharp\ turn \end{cases} ⎩ ⎨ ⎧ 1. n o t co n t in u o u s 2. v er t i c a l t an g e t 3. s ha r p t u r n
P r o o f . \mathnormal{Proof.} P roo f .
A s s u m e : f d i f f e r e n t i a b i l i t y a t x = c Assume:\ f\ differentiability\ at\ x=c A ss u m e : f d i ff ere n t iabi l i t y a t x = c
∵ f d i f f e r e n t i a b i l i t y a t x = c ∴ f ′ ( c ) = lim x → c f ( x ) − f ( c ) x − c \begin{array}{l} \because f\ differentiability\ at\ x=c\\ \therefore \displaystyle f^{\prime }( c) = \lim _{x\rightarrow c}\frac{f( x) -f( c)}{x-c} \end{array} ∵ f d i ff ere n t iabi l i t y a t x = c ∴ f ′ ( c ) = x → c lim x − c f ( x ) − f ( c )
lim x → c [ f ( x ) − f ( c ) ] = lim x → c ( x − c ) ⋅ f ( x ) − f ( c ) x − c = lim x → c ( x − c ) ⋅ lim x → c f ( x ) − f ( c ) x − c = 0 ⋅ f ′ ( c ) = 0 lim x → c [ f ( x ) − f ( c ) ] = 0 lim x → c f ( x ) − lim x → c f ( c ) = 0 lim x → c f ( x ) − f ( c ) = 0 lim x → c f ( x ) = f ( c ) Q . E . D . \begin{aligned} \lim _{x\rightarrow c}[ f( x) -f( c)] & =\lim _{x\rightarrow c}( x-c) \cdot \frac{f( x) -f( c)}{x-c}\\ & =\lim _{x\rightarrow c}( x-c) \cdot \lim _{x\rightarrow c}\frac{f( x) -f( c)}{x-c}\\ & =0\cdot f^{\prime }( c)\\ & =0\\ & \\ \lim _{x\rightarrow c}[ f( x) -f( c)] & =0\\ \lim _{x\rightarrow c} f( x) -\lim _{x\rightarrow c} f( c) & =0\\ \lim _{x\rightarrow c} f( x) -f( c) & =0\\ \lim _{x\rightarrow c} f( x) & =f( c) & Q.E.D. \end{aligned} x → c lim [ f ( x ) − f ( c )] x → c lim [ f ( x ) − f ( c )] x → c lim f ( x ) − x → c lim f ( c ) x → c lim f ( x ) − f ( c ) x → c lim f ( x ) = x → c lim ( x − c ) ⋅ x − c f ( x ) − f ( c ) = x → c lim ( x − c ) ⋅ x → c lim x − c f ( x ) − f ( c ) = 0 ⋅ f ′ ( c ) = 0 = 0 = 0 = 0 = f ( c ) Q . E . D . P r o o f . \mathnormal{Proof.} P roo f .
d d x ( x n ) = lim Δ x → 0 ( x + Δ x ) n − x n Δ x \displaystyle \frac{d}{dx}\left( x^{n}\right) =\lim _{\Delta x\rightarrow 0}\frac{( x+\Delta x)^{n} -x^{n}}{\Delta x} d x d ( x n ) = Δ x → 0 lim Δ x ( x + Δ x ) n − x n
A c c o r d i n g t o B i n o m i a l t h e o r e m : According\ to\ Binomial\ theorem: A ccor d in g t o B in o mia l t h eore m :
lim Δ x → 0 ( x + Δ x ) n − x n Δ x = lim Δ x → 0 x n + ( n 1 ) x n − 1 Δ x + ( n 2 ) x n − 2 Δ x 2 + . . . + ( n n ) x 0 Δ x n − x n Δ x = lim Δ x → 0 ( n 1 ) x n − 1 + ( n 2 ) x n − 2 Δ x + . . . + ( n n ) Δ x n − 1 = lim Δ x → 0 ( n 1 ) x n − 1 = lim Δ x → 0 n ! 1 ! ( n − 1 ) ! x n − 1 = lim Δ x → 0 n x n − 1 Q . E . D . \begin{aligned} \displaystyle \lim _{\Delta x\rightarrow 0}\frac{( x+\Delta x)^{n} -x^{n}}{\Delta x} & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\cancel{x^{n}} +\binom{n}{1} x^{n-1} \Delta x+\binom{n}{2} x^{n-2} \Delta x^{2} +...+\binom{n}{n} x^{0} \Delta x^{n}\cancel{-x^{n}}}{\Delta x}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\binom{n}{1} x^{n-1} +\cancel{\binom{n}{2} x^{n-2} \Delta x} +...+\cancel{\binom{n}{n} \Delta x^{n-1}}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\binom{n}{1} x^{n-1}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{n!}{\cancel{1!}( n-1) !} x^{n-1}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0} nx^{n-1} & Q.E.D. \end{aligned} Δ x → 0 lim Δ x ( x + Δ x ) n − x n = Δ x → 0 lim Δ x x n + ( 1 n ) x n − 1 Δ x + ( 2 n ) x n − 2 Δ x 2 + ... + ( n n ) x 0 Δ x n − x n = Δ x → 0 lim ( 1 n ) x n − 1 + ( 2 n ) x n − 2 Δ x + ... + ( n n ) Δ x n − 1 = Δ x → 0 lim ( 1 n ) x n − 1 = Δ x → 0 lim 1 ! ( n − 1 )! n ! x n − 1 = Δ x → 0 lim n x n − 1 Q . E . D . P r o o f . \mathnormal{Proof.} P roo f .
d d x ( x ) = lim Δ x → 0 x + Δ x − x Δ x = lim Δ x → 0 ( x + Δ x − x ) ( x + Δ x + x ) Δ x ( x + Δ x + x ) = lim Δ x → 0 1 x + Δ x + x = lim Δ x → 0 1 2 x = lim Δ x → 0 1 2 x − 1 2 Q . E . D . \begin{aligned} \frac{d}{dx}\left(\sqrt{x}\right) & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\sqrt{x+\Delta x} -\sqrt{x}}{\Delta x}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\left(\sqrt{x+\Delta x} -\sqrt{x}\right)\left(\sqrt{x+\Delta x} +\sqrt{x}\right)}{\Delta x\left(\sqrt{x+\Delta x} +\sqrt{x}\right)}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{1}{\sqrt{x+\Delta x} +\sqrt{x}}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{1}{2\sqrt{x}}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{1}{2} x^{-\frac{1}{2}} & Q.E.D. \end{aligned} d x d ( x ) = Δ x → 0 lim Δ x x + Δ x − x = Δ x → 0 lim Δ x ( x + Δ x + x ) ( x + Δ x − x ) ( x + Δ x + x ) = Δ x → 0 lim x + Δ x + x 1 = Δ x → 0 lim 2 x 1 = Δ x → 0 lim 2 1 x − 2 1 Q . E . D . P r o o f . \mathnormal{Proof.} P roo f .
∵ k i s c o n s t a n t ∴ y d o e s n o t c h a n g e a s x c h a n g e s ∴ f ( x + h ) − f ( x ) = 0 ∴ d d x k = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 0 h = 0 \begin{array}{l} \because k\ is\ constant\\ \therefore y\ does\ not\ change\ as\ x\ changes\\ \therefore f( x+h) -f( x) =0\\ \therefore \displaystyle \frac{d}{dx} k= \lim _{h\rightarrow 0}\frac{f( x+h) -f( x)}{h} =\lim _{h\rightarrow 0}\frac{0}{h} =0 \end{array} ∵ k i s co n s t an t ∴ y d oes n o t c han g e a s x c han g es ∴ f ( x + h ) − f ( x ) = 0 ∴ d x d k = h → 0 lim h f ( x + h ) − f ( x ) = h → 0 lim h 0 = 0 Constant multiple rule: d d x [ k ⋅ f ( x ) ] = k ⋅ d d x f ( x ) \displaystyle \dfrac{d}{dx}[k\cdot f(x)]=k\cdot\dfrac{d}{dx}f(x) d x d [ k ⋅ f ( x )] = k ⋅ d x d f ( x )
Sum rule: d d x [ f ( x ) + g ( x ) ] = d d x f ( x ) + d d x g ( x ) \displaystyle \dfrac{d}{dx}[f(x)+g(x)]=\dfrac{d}{dx}f(x)+\dfrac{d}{dx}g(x) d x d [ f ( x ) + g ( x )] = d x d f ( x ) + d x d g ( x )
Difference rule: d d x [ f ( x ) − g ( x ) ] = d d x f ( x ) − d d x g ( x ) \displaystyle \dfrac{d}{dx}[f(x)-g(x)]=\dfrac{d}{dx}f(x)-\dfrac{d}{dx}g(x) d x d [ f ( x ) − g ( x )] = d x d f ( x ) − d x d g ( x )
P r o o f . \mathnormal{Proof.} P roo f .
1. f ( x ) = k g ( x ) ⟹ f ′ ( x ) = k g ′ ( x ) \displaystyle 1.\ f( x) =kg( x) \Longrightarrow f^{\prime }( x) =kg^{\prime }( x) 1. f ( x ) = k g ( x ) ⟹ f ′ ( x ) = k g ′ ( x )
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 k g ( x + h ) − k g ( x ) h = lim h → 0 k ( g ( x + h ) − g ( x ) h ) = k lim h → 0 g ( x + h ) − g ( x ) h = k g ′ ( x ) Q . E . D . \begin{aligned} f^{\prime }( x) & =\displaystyle \lim _{h\rightarrow 0}\frac{f( x+h) -f( x)}{h}\\ & =\displaystyle \lim _{h\rightarrow 0}\frac{kg( x+h) -kg( x)}{h}\\ & =\displaystyle \lim _{h\rightarrow 0} k\left(\frac{g( x+h) -g( x)}{h}\right)\\ & =k\displaystyle \lim _{h\rightarrow 0}\frac{g( x+h) -g( x)}{h}\\ & =kg^{\prime }( x) & Q.E.D. \end{aligned} f ′ ( x ) = h → 0 lim h f ( x + h ) − f ( x ) = h → 0 lim h k g ( x + h ) − k g ( x ) = h → 0 lim k ( h g ( x + h ) − g ( x ) ) = k h → 0 lim h g ( x + h ) − g ( x ) = k g ′ ( x ) Q . E . D . 2. f ( x ) = g ( x ) ± j ( x ) ⟹ f ′ ( x ) = g ′ ( x ) ± j ′ ( x ) \displaystyle 2.\ f( x) =g( x) \pm j( x) \Longrightarrow f^{\prime }( x) =g^{\prime }( x) \pm j^{\prime }( x) 2. f ( x ) = g ( x ) ± j ( x ) ⟹ f ′ ( x ) = g ′ ( x ) ± j ′ ( x )
f ′ ( x ) = lim h → 0 g ( x + h ) ± j ( x + h ) − ( g ( x ) ± j ( x ) ) h = lim h → 0 ( g ( x + h ) − g ( x ) h ± j ( x + h ) − j ( x ) h ) = lim h → 0 g ( x + h ) − g ( x ) h ± lim h → 0 j ( x + h ) − j ( x ) h = g ′ ( x ) ± j ′ ( x ) Q . E . D . \begin{aligned} f^{\prime }( x) & =\displaystyle \lim _{h\rightarrow 0}\frac{g( x+h) \pm j( x+h) -( g( x) \pm j( x))}{h}\\ & =\displaystyle \lim _{h\rightarrow 0}\left(\frac{g( x+h) -g( x)}{h} \pm \frac{j( x+h) -j( x)}{h}\right)\\ & =\displaystyle \lim _{h\rightarrow 0}\frac{g( x+h) -g( x)}{h} \pm \lim _{h\rightarrow 0}\frac{j( x+h) -j( x)}{h}\\ & =g^{\prime }( x) \pm j^{\prime }( x) & Q.E.D. \end{aligned} f ′ ( x ) = h → 0 lim h g ( x + h ) ± j ( x + h ) − ( g ( x ) ± j ( x )) = h → 0 lim ( h g ( x + h ) − g ( x ) ± h j ( x + h ) − j ( x ) ) = h → 0 lim h g ( x + h ) − g ( x ) ± h → 0 lim h j ( x + h ) − j ( x ) = g ′ ( x ) ± j ′ ( x ) Q . E . D . Known lim x → 0 sin x x = 1 \displaystyle \lim _{x\rightarrow 0}\frac{\sin x}{x} =1 x → 0 lim x sin x = 1 lim x → 0 1 − cos x x = 0 \displaystyle \lim _{x\rightarrow 0}\frac{1-\cos x}{x} =0 x → 0 lim x 1 − cos x = 0
P r o o f . \mathnormal{Proof.} P roo f .
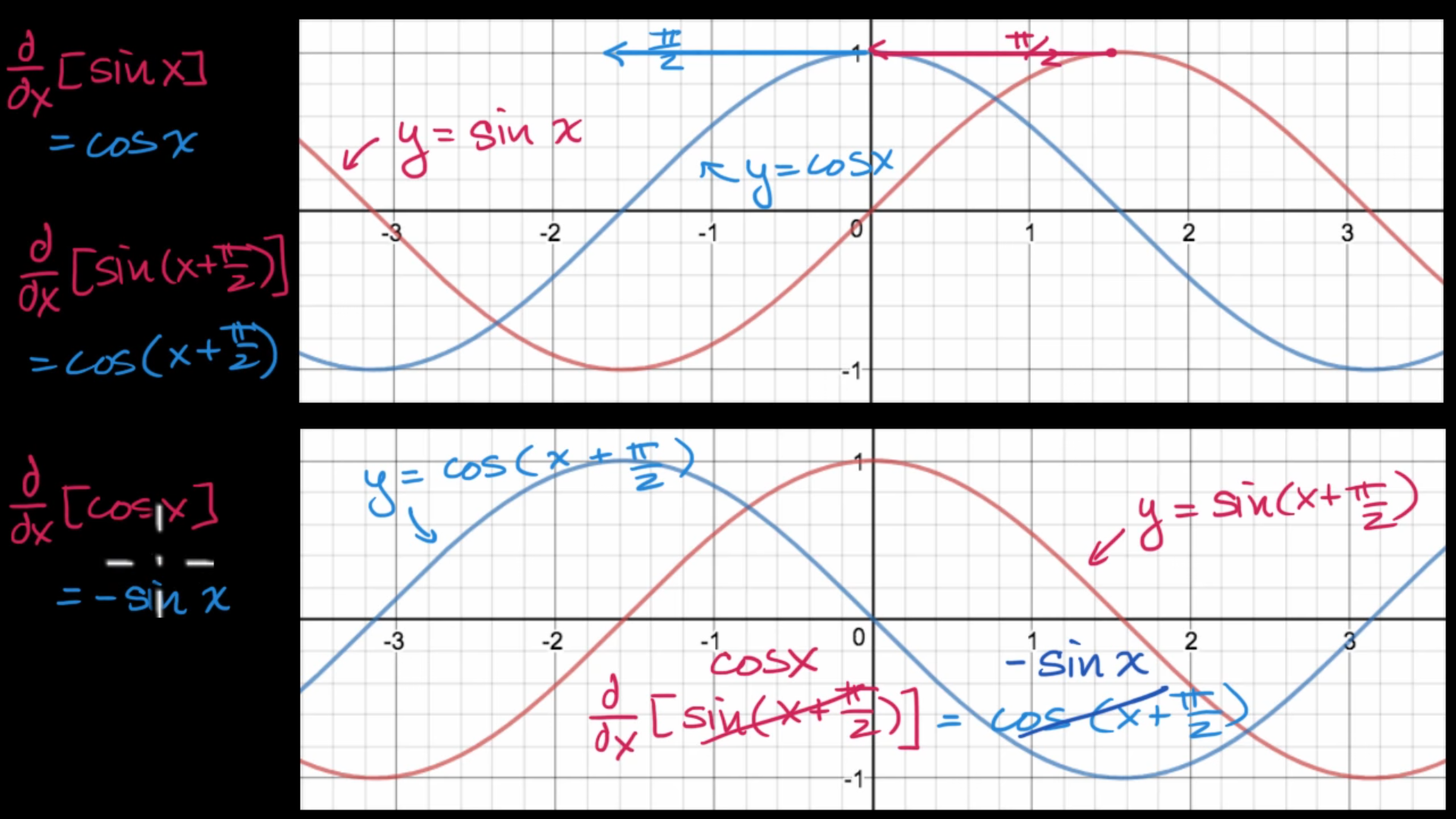
1. d d x [ sin x ] = cos x \displaystyle 1.\ \frac{d}{dx}[\sin x] =\cos x 1. d x d [ sin x ] = cos x
d d x [ sin x ] = lim Δ x → 0 sin ( x + Δ x ) − sin ( x ) Δ x = lim Δ x → 0 cos x sin Δ x + sin x cos Δ x − sin x Δ x = lim Δ x → 0 ( cos x sin Δ x Δ x + sin x cos Δ x − sin x Δ x ) = lim Δ x → 0 cos x ( sin Δ x Δ x ) + lim Δ x → 0 sin x ( cos Δ x − 1 ) Δ x = cos x lim Δ x → 0 sin Δ x Δ x − sin x lim Δ x → 0 1 − cos Δ x Δ x = cos x ⋅ 1 − sin x ⋅ 0 = cos x Q . E . D . \begin{aligned} \frac{d}{dx}[\sin x] & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\sin( x+\Delta x) -\sin( x)}{\Delta x}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\cos x\sin \Delta x+\sin x\cos \Delta x-\sin x}{\Delta x}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\left(\frac{\cos x\sin \Delta x}{\Delta x} +\frac{\sin x\cos \Delta x-\sin x}{\Delta x}\right)\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\cos x\left(\frac{\sin \Delta x}{\Delta x}\right) +\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\sin x(\cos \Delta x-1)}{\Delta x}\\ & =\cos x\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\sin \Delta x}{\Delta x} -\sin x\displaystyle \lim _{\Delta x\rightarrow 0}\frac{1-\cos \Delta x}{\Delta x}\\ & =\cos x\cdot 1-\sin x\cdot 0\\ & =\cos x & Q.E.D. \end{aligned} d x d [ sin x ] = Δ x → 0 lim Δ x sin ( x + Δ x ) − sin ( x ) = Δ x → 0 lim Δ x cos x sin Δ x + sin x cos Δ x − sin x = Δ x → 0 lim ( Δ x cos x sin Δ x + Δ x sin x cos Δ x − sin x ) = Δ x → 0 lim cos x ( Δ x sin Δ x ) + Δ x → 0 lim Δ x sin x ( cos Δ x − 1 ) = cos x Δ x → 0 lim Δ x sin Δ x − sin x Δ x → 0 lim Δ x 1 − cos Δ x = cos x ⋅ 1 − sin x ⋅ 0 = cos x Q . E . D . 2. d d x [ cos x ] = − sin x \displaystyle 2.\ \frac{d}{dx}[\cos x] =-\sin x 2. d x d [ cos x ] = − sin x
Know the limit definition of e \mathbb{e} e e = lim n → ∞ ( 1 + 1 n ) n = lim n → 0 ( 1 + n ) 1 n e=\displaystyle \lim _{n\rightarrow \infty }\left( 1+\frac{1}{n}\right)^{n} =\displaystyle \lim _{n\rightarrow 0}( 1+n)^{\frac{1}{n}} e = n → ∞ lim ( 1 + n 1 ) n = n → 0 lim ( 1 + n ) n 1
P r o o f . \mathnormal{Proof.} P roo f .
d d x ( e x ) = lim Δ x → 0 e x + Δ x − e x Δ x = e x lim Δ x → 0 e Δ x − 1 Δ x \begin{aligned} \frac{d}{dx}\left( e^{x}\right) & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{e^{x+\Delta x} -e^{x}}{\Delta x}\\ & =e^{x}\displaystyle \lim _{\Delta x\rightarrow 0}\frac{e^{\Delta x} -1}{\Delta x} \end{aligned} d x d ( e x ) = Δ x → 0 lim Δ x e x + Δ x − e x = e x Δ x → 0 lim Δ x e Δ x − 1 L e t n = e Δ x − 1 , w e c a n g e t n + 1 = e Δ x , s u c h t h a t Δ x = ln ( n + 1 ) a n d a s Δ x → 0 = n → 0 \displaystyle Let\ n=e^{\Delta x} -1,\ we\ can\ get\ n+1=e^{\Delta x} ,\ such\ that\ \Delta x=\ln( n+1) \ and\ as\ \Delta x\rightarrow 0=n\rightarrow 0 L e t n = e Δ x − 1 , w e c an g e t n + 1 = e Δ x , s u c h t ha t Δ x = ln ( n + 1 ) an d a s Δ x → 0 = n → 0
W e c a n r e w r i t e t o : We\ can\ rewrite\ to: W e c an re w r i t e t o :
d d x ( e x ) = e x lim n → 0 n ln ( n + 1 ) = e x lim n → 0 1 n n 1 n ln ( n + 1 ) = e x lim n → 0 1 ln [ ( 1 + n ) 1 n ] = e x 1 ln [ lim n → 0 ( 1 + n ) 1 n ] = e x Q . E . D . \begin{aligned} \frac{d}{dx}\left( e^{x}\right) & =e^{x}\displaystyle \lim _{n\rightarrow 0}\frac{n}{\ln( n+1)}\\ & =e^{x}\displaystyle \lim _{n\rightarrow 0}\frac{\frac{1}{n} n}{\frac{1}{n}\ln( n+1)}\\ & =e^{x}\displaystyle \lim _{n\rightarrow 0}\frac{1}{\ln\left[( 1+n)^{\frac{1}{n}}\right]}\\ & =e^{x}\frac{1}{\ln\left[\displaystyle \lim _{n\rightarrow 0}( 1+n)^{\frac{1}{n}}\right]}\\ & =e^{x} & Q.E.D. \end{aligned} d x d ( e x ) = e x n → 0 lim ln ( n + 1 ) n = e x n → 0 lim n 1 ln ( n + 1 ) n 1 n = e x n → 0 lim ln [ ( 1 + n ) n 1 ] 1 = e x ln [ n → 0 lim ( 1 + n ) n 1 ] 1 = e x Q . E . D . P r o o f . \mathnormal{Proof.} P roo f .
d d x ( ln x ) = lim Δ x → 0 ln ( x + Δ x ) − ln ( x ) Δ x = lim Δ x → 0 ln ( x + Δ x x ) Δ x = lim Δ x → 0 ln ( 1 + Δ x x ) Δ x = lim Δ x → 0 1 Δ x ln ( 1 + Δ x x ) = lim Δ x → 0 ln [ ( 1 + Δ x x ) 1 Δ x ] \begin{aligned} \frac{d}{dx}(\ln x) & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\ln( x+\Delta x) -\ln( x)}{\Delta x}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\ln\left(\frac{x+\Delta x}{x}\right)}{\Delta x}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\ln\left( 1+\frac{\Delta x}{x}\right)}{\Delta x}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{1}{\Delta x}\ln\left( 1+\frac{\Delta x}{x}\right)\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\ln\left[\left( 1+\frac{\Delta x}{x}\right)^{\frac{1}{\Delta x}}\right] \end{aligned} d x d ( ln x ) = Δ x → 0 lim Δ x ln ( x + Δ x ) − ln ( x ) = Δ x → 0 lim Δ x ln ( x x + Δ x ) = Δ x → 0 lim Δ x ln ( 1 + x Δ x ) = Δ x → 0 lim Δ x 1 ln ( 1 + x Δ x ) = Δ x → 0 lim ln [ ( 1 + x Δ x ) Δ x 1 ] L e t n = Δ x x , Δ x = n x , 1 Δ x = 1 n ⋅ 1 x a n d a s Δ x → 0 = n → 0 \displaystyle Let\ n=\frac{\Delta x}{x} ,\ \Delta x=nx,\ \frac{1}{\Delta x} =\frac{1}{n} \cdot \frac{1}{x} \ and\ as\ \Delta x\rightarrow 0=n\rightarrow 0 L e t n = x Δ x , Δ x = n x , Δ x 1 = n 1 ⋅ x 1 an d a s Δ x → 0 = n → 0
W e c a n r e w r i t e t o : We\ can\ rewrite\ to: W e c an re w r i t e t o :
lim Δ x → 0 ln [ ( 1 + Δ x x ) 1 Δ x ] = 1 x lim n → 0 ln [ ( 1 + n ) 1 n ] = 1 x ln [ lim n → 0 ( 1 + n ) 1 n ] = 1 x Q . E . D . \begin{aligned} \displaystyle \lim _{\Delta x\rightarrow 0}\ln\left[\left( 1+\frac{\Delta x}{x}\right)^{\frac{1}{\Delta x}}\right] & =\frac{1}{x}\displaystyle \lim _{n\rightarrow 0}\ln\left[( 1+n)^{\frac{1}{n}}\right]\\ & =\frac{1}{x}\ln\left[\displaystyle \lim _{n\rightarrow 0}( 1+n)^{\frac{1}{n}}\right]\\ & =\frac{1}{x} & Q.E.D. \end{aligned} Δ x → 0 lim ln [ ( 1 + x Δ x ) Δ x 1 ] = x 1 n → 0 lim ln [ ( 1 + n ) n 1 ] = x 1 ln [ n → 0 lim ( 1 + n ) n 1 ] = x 1 Q . E . D . d d x ( e x ) = e x \displaystyle \frac{d}{dx}\left( e^{x}\right) =e^{x} d x d ( e x ) = e x P r o o f . \mathnormal{Proof.} P roo f .
K n o w n d d x ( e x ) = e x \displaystyle Known\ \frac{d}{dx}\left( e^{x}\right) =e^{x} K n o w n d x d ( e x ) = e x
L e t y = ln ( x ) , w e c a n g e t : \displaystyle Let\ y=\ln( x) ,\ we\ can\ get: L e t y = ln ( x ) , w e c an g e t :
d d x ( e y ) = d d x ( x ) e y ⋅ d y d x = 1 d y d x = 1 e y = 1 e ln x = 1 x Q . E . D . \begin{aligned} \frac{d}{dx}\left( e^{y}\right) & =\frac{d}{dx}( x)\\ e^{y} \cdot \frac{dy}{dx} & =1\\ \frac{dy}{dx} & =\frac{1}{e^{y}}\\ & =\frac{1}{e^{\ln x}}\\ & =\frac{1}{x} & Q.E.D. \end{aligned} d x d ( e y ) e y ⋅ d x d y d x d y = d x d ( x ) = 1 = e y 1 = e l n x 1 = x 1 Q . E . D . P r o o f . \mathnormal{Proof.} P roo f .
d d x [ f ( x ) g ( x ) ] = lim h → 0 f ( x + h ) g ( x + h ) − f ( x + h ) g ( x ) + f ( x + h ) g ( x ) − f ( x ) g ( x ) h = lim h → 0 [ f ( x + h ) g ( x + h ) − g ( x ) h + g ( x ) f ( x + h ) − f ( x ) h ] = [ lim h → 0 f ( x + h ) ] [ lim h → 0 g ( x + h ) − g ( x ) h ] + [ lim h → 0 g ( x ) ] [ lim h → 0 f ( x + h ) − f ( x ) h ] = f ( x ) g ′ ( x ) + g ( x ) f ′ ( x ) Q . E . D . \begin{aligned} \frac{d}{dx}[ f( x) g( x)] & =\displaystyle \lim _{h\rightarrow 0}\frac{f( x+h) g( x+h) -f( x+h) g( x) +f( x+h) g( x) -f( x) g( x)}{h}\\ & =\displaystyle \lim _{h\rightarrow 0}\left[ f( x+h)\frac{g( x+h) -g( x)}{h} +g( x)\frac{f( x+h) -f( x)}{h}\right]\\ & =\left[\displaystyle \lim _{h\rightarrow 0} f( x+h)\right]\left[\displaystyle \lim _{h\rightarrow 0}\frac{g( x+h) -g( x)}{h}\right] +\left[\displaystyle \lim _{h\rightarrow 0} g( x)\right]\left[\displaystyle \lim _{h\rightarrow 0}\frac{f( x+h) -f( x)}{h}\right]\\ & =f( x) g^{\prime }( x) +g( x) f^{\prime }( x) & Q.E.D. \end{aligned} d x d [ f ( x ) g ( x )] = h → 0 lim h f ( x + h ) g ( x + h ) − f ( x + h ) g ( x ) + f ( x + h ) g ( x ) − f ( x ) g ( x ) = h → 0 lim [ f ( x + h ) h g ( x + h ) − g ( x ) + g ( x ) h f ( x + h ) − f ( x ) ] = [ h → 0 lim f ( x + h ) ] [ h → 0 lim h g ( x + h ) − g ( x ) ] + [ h → 0 lim g ( x ) ] [ h → 0 lim h f ( x + h ) − f ( x ) ] = f ( x ) g ′ ( x ) + g ( x ) f ′ ( x ) Q . E . D . tan ( x ) \tan( x) tan ( x ) cos ( x ) \cos( x) cos ( x ) sec ( x ) \sec( x) sec ( x ) csc ( x ) \csc( x) csc ( x ) P r o o f . \mathnormal{Proof.} P roo f .
d d x ( tan x ) = d d x ( sin x cos x ) d d x ( cot x ) = d d x ( cos x sin x ) = cos 2 x + sin 2 x cos 2 x = − ( sin 2 x + cos 2 x ) sin 2 x = 1 cos 2 x = − 1 sin 2 x = sec 2 x = − csc 2 x d d x ( sec x ) = d d x ( 1 cos x ) d d x ( csc x ) = d d x ( 1 sin x ) = 0 ⋅ cos x + 1 ⋅ sin x cos 2 x = 0 ⋅ sin x − 1 ⋅ cos x sin 2 x = sin x cos 2 x = − cos x sin 2 x = tan x ⋅ sec x = − cot x ⋅ csc x Q . E . D . \begin{aligned} \frac{d}{dx}(\tan x) & =\frac{d}{dx}\left(\frac{\sin x}{\cos x}\right) & \frac{d}{dx}(\cot x) & =\frac{d}{dx}\left(\frac{\cos x}{\sin x}\right)\\ & =\frac{\cos^{2} x+\sin^{2} x}{\cos^{2} x} & & =\frac{-\left(\sin^{2} x+\cos^{2} x\right)}{\sin^{2} x}\\ & =\frac{1}{\cos^{2} x} & & =-\frac{1}{\sin^{2} x}\\ & =\sec^{2} x & & =-\csc^{2} x\\ \frac{d}{dx}(\sec x) & =\frac{d}{dx}\left(\frac{1}{\cos x}\right) & \frac{d}{dx}(\csc x) & =\frac{d}{dx}\left(\frac{1}{\sin x}\right)\\ & =\frac{0\cdot \cos x+1\cdot \sin x}{\cos^{2} x} & & =\frac{0\cdot \sin x-1\cdot \cos x}{\sin^{2} x}\\ & =\frac{\sin x}{\cos^{2} x} & & =-\frac{\cos x}{\sin^{2} x}\\ & =\tan x\cdot \sec x & & =-\cot x\cdot \csc x & Q.E.D. \end{aligned} d x d ( tan x ) d x d ( sec x ) = d x d ( cos x sin x ) = cos 2 x cos 2 x + sin 2 x = cos 2 x 1 = sec 2 x = d x d ( cos x 1 ) = cos 2 x 0 ⋅ cos x + 1 ⋅ sin x = cos 2 x sin x = tan x ⋅ sec x d x d ( cot x ) d x d ( csc x ) = d x d ( sin x cos x ) = sin 2 x − ( sin 2 x + cos 2 x ) = − sin 2 x 1 = − csc 2 x = d x d ( sin x 1 ) = sin 2 x 0 ⋅ sin x − 1 ⋅ cos x = − sin 2 x cos x = − cot x ⋅ csc x Q . E . D . P r o o f . \mathnormal{Proof.} P roo f .
K n o w n d d x ( e x ) = e x \displaystyle Known\ \frac{d}{dx}\left( e^{x}\right) =e^{x} K n o w n d x d ( e x ) = e x
L e t a = e ln a \displaystyle Let\ a=e^{\ln a} L e t a = e l n a
d d x ( a x ) = d d x [ ( e ln a ) x ] = d d x [ e ( ln a ) x ] = e ( ln a ) x ⋅ ln a = a x ⋅ ln a Q . E . D . \begin{aligned} \frac{d}{dx}\left( a^{x}\right) & =\frac{d}{dx}\left[\left( e^{\ln a}\right)^{x}\right]\\ & =\frac{d}{dx}\left[ e^{(\ln a) x}\right]\\ & =e^{(\ln a) x} \cdot \ln a\\ & =a^{x} \cdot \ln a & Q.E.D. \end{aligned} d x d ( a x ) = d x d [ ( e l n a ) x ] = d x d [ e ( l n a ) x ] = e ( l n a ) x ⋅ ln a = a x ⋅ ln a Q . E . D . P r o o f . \mathnormal{Proof.} P roo f .
K n o w n d d x ( ln x ) = 1 x \displaystyle Known\ \frac{d}{dx}(\ln x) =\frac{1}{x} K n o w n d x d ( ln x ) = x 1
d d x ( log a x ) = d d x ( 1 ln a ⋅ ln x ) = 1 x ln a Q . E . D . \begin{aligned} \frac{d}{dx}(\log_{a} x) & =\frac{d}{dx}\left(\frac{1}{\ln a} \cdot \ln x\right)\\ & =\frac{1}{x\ln a} & Q.E.D. \end{aligned} d x d ( log a x ) = d x d ( ln a 1 ⋅ ln x ) = x ln a 1 Q . E . D . C h a i n R u l e P r o o f . \mathnormal{Chain\ Rule\ Proof.} C hain R u l e P roo f .
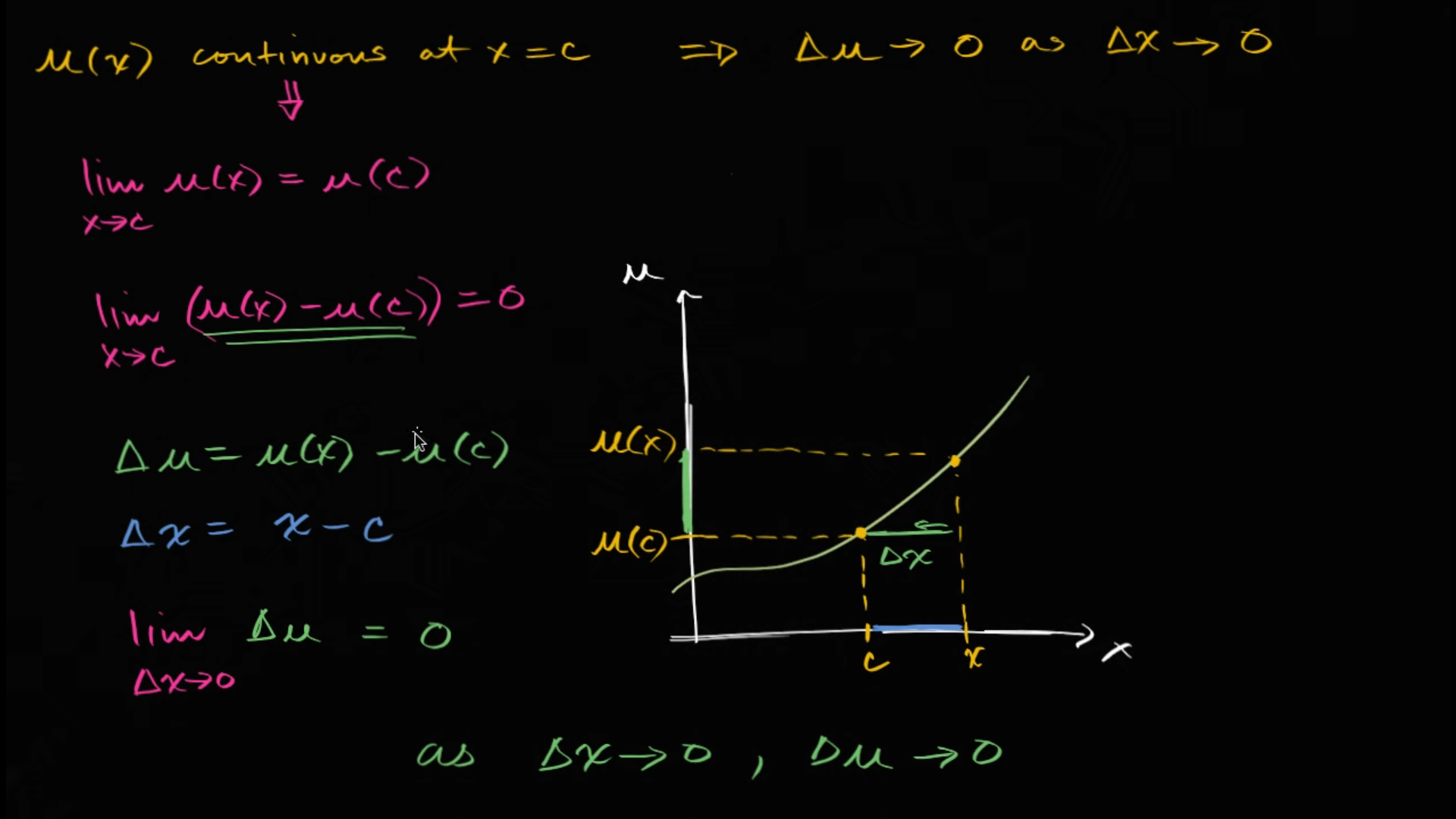
K n o w n : 1. I f a f u n c t i o n i s d i f f e r e n t i a b l e , t h e n i t i s a l s o c o n t i n u o u s . 2. I f f u n c t i o n u i s c o n t i n u o u s a t x , t h e n Δ u → 0 a s Δ x → 0 \begin{aligned} Known:\ & 1.\ If\ a\ function\ is\ differentiable,\ then\ it\ is\ also\ continuous.\\ & 2.\ If\ function\ u\ is\ continuous\ at\ x,\ then\ \Delta u\rightarrow 0\ as\ \Delta x\rightarrow 0 \end{aligned} K n o w n : 1. I f a f u n c t i o n i s d i ff ere n t iab l e , t h e n i t i s a l so co n t in u o u s . 2. I f f u n c t i o n u i s co n t in u o u s a t x , t h e n Δ u → 0 a s Δ x → 0 F o r w h y i f f u n c t i o n u i s c o n t i n u o u s a t x , t h e n Δ u → 0 a s Δ x → 0 For\ why\ if\ function\ u\ is\ continuous\ at\ x,\ then\ \Delta u\rightarrow 0\ as\ \Delta x\rightarrow 0 F or w h y i f f u n c t i o n u i s co n t in u o u s a t x , t h e n Δ u → 0 a s Δ x → 0
T h e c h a i n r u l e t e l l u s : d d x [ y ( u ( x ) ) ] = d y d x = d y d u ⋅ d u d x \displaystyle The\ chain\ rule\ tell\ us:\ \frac{d}{dx}[ y( u( x))] =\frac{dy}{dx} =\frac{dy}{du} \cdot \frac{du}{dx} T h e c hain r u l e t e ll u s : d x d [ y ( u ( x ))] = d x d y = d u d y ⋅ d x d u
A s s u m i n g y , u d i f f e r e n t i a b l e a t x . W e c a n g e t : Assuming\ y,\ u\ differentiable\ at\ x.\ We\ can\ get: A ss u min g y , u d i ff ere n t iab l e a t x . W e c an g e t :
d y d x = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 Δ y Δ u ⋅ Δ u Δ x = ( lim Δ x → 0 Δ y Δ u ) ( lim Δ x → 0 Δ u Δ x ) = ( lim Δ u → 0 Δ y Δ u ) ( lim Δ x → 0 Δ u Δ x ) = d y d u ⋅ d u d x Q . E . D . \begin{aligned} \frac{dy}{dx} & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}\\ & =\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta u} \cdot \frac{\Delta u}{\Delta x}\\ & =\left(\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta u}\right)\left(\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\Delta u}{\Delta x}\right)\\ & =\left(\displaystyle \lim _{\Delta u\rightarrow 0}\frac{\Delta y}{\Delta u}\right)\left(\displaystyle \lim _{\Delta x\rightarrow 0}\frac{\Delta u}{\Delta x}\right)\\ & =\frac{dy}{du} \cdot \frac{du}{dx} & Q.E.D. \end{aligned} d x d y = Δ x → 0 lim Δ x Δ y = Δ x → 0 lim Δ u Δ y ⋅ Δ x Δ u = ( Δ x → 0 lim Δ u Δ y ) ( Δ x → 0 lim Δ x Δ u ) = ( Δ u → 0 lim Δ u Δ y ) ( Δ x → 0 lim Δ x Δ u ) = d u d y ⋅ d x d u Q . E . D . Q u o t i e n t R u l e P r o o f . \mathnormal{Quotient\ Rule\ Proof.} Q u o t i e n t R u l e P roo f .
d d x [ f ( x ) g ( x ) ] = d d x [ f ( x ) ⋅ [ g ( x ) ] − 1 ] = f ′ ( x ) [ g ( x ) ] − 1 − f ( x ) [ g ( x ) ] − 2 g ′ ( x ) = f ′ ( x ) g ( x ) − f ( x ) g ′ ( x ) [ g ( x ) ] 2 = f ′ ( x ) g ( x ) − f ( x ) g ′ ( x ) [ g ( x ) ] 2 Q . E . D . \begin{aligned} \frac{d}{dx}\left[\frac{f( x)}{g( x)}\right] & =\frac{d}{dx}\left[ f( x) \cdot [ g( x)]^{-1}\right]\\ & =f^{\prime }( x)[ g( x)]^{-1} -f( x)[ g( x)]^{-2} g^{\prime }( x)\\ & =\frac{f^{\prime }( x)}{g( x)} -\frac{f( x) g^{\prime }( x)}{[ g( x)]^{2}}\\ & =\frac{f^{\prime }( x) g( x) -f( x) g^{\prime }( x)}{[ g( x)]^{2}} & Q.E.D. \end{aligned} d x d [ g ( x ) f ( x ) ] = d x d [ f ( x ) ⋅ [ g ( x ) ] − 1 ] = f ′ ( x ) [ g ( x ) ] − 1 − f ( x ) [ g ( x ) ] − 2 g ′ ( x ) = g ( x ) f ′ ( x ) − [ g ( x ) ] 2 f ( x ) g ′ ( x ) = [ g ( x ) ] 2 f ′ ( x ) g ( x ) − f ( x ) g ′ ( x ) Q . E . D .
This isn't full proof of L'Hôpital's rule, just a special case. But it should give some intuition for why it works.
f ( a ) = 0 , g ( a ) = 0 ; f ′ ( a ) e x i s t s , g ′ ( a ) e x i s t s ⟺ lim x → a f ( x ) g ( x ) = f ′ ( a ) g ′ ( a ) f( a) =0,\ g( a) =0;\ f^{\prime} ( a) \ exists,\ g^{\prime} ( a) \ exists\ \Longleftrightarrow \ \displaystyle \lim _{x\rightarrow a}\frac{f( x)}{g( x)} =\frac{f^{\prime} ( a)}{g^{\prime} ( a)} f ( a ) = 0 , g ( a ) = 0 ; f ′ ( a ) e x i s t s , g ′ ( a ) e x i s t s ⟺ x → a lim g ( x ) f ( x ) = g ′ ( a ) f ′ ( a ) f ′ ( a ) g ′ ( a ) = lim x → a f ( x ) − f ( a ) x − a lim x → a g ( x ) − g ( a ) x − a = lim x → a f ( x ) − f ( a ) g ( x ) − g ( a ) = lim x → a f ( x ) g ( x ) W e k n o w f ( a ) a n d g ( a ) b o t h e q u a l t o z e r o Q . E . D \begin{aligned} \frac{f^{\prime }( a)}{g^{\prime }( a)} & =\frac{\displaystyle \lim _{x\rightarrow a}\frac{f( x) -f( a)}{x-a}}{\displaystyle \lim _{x\rightarrow a}\frac{g( x) -g( a)}{x-a}} & \\ & =\displaystyle \lim _{x\rightarrow a}\frac{f( x) -f( a)}{g( x) -g( a)} & \\ & =\displaystyle \lim _{x\rightarrow a}\frac{f( x)}{g( x)} & We\ know\ f( a) \ and\ g( a) \ both\ equal\ to\ zero \\ & & Q.E.D \end{aligned} g ′ ( a ) f ′ ( a ) = x → a lim x − a g ( x ) − g ( a ) x → a lim x − a f ( x ) − f ( a ) = x → a lim g ( x ) − g ( a ) f ( x ) − f ( a ) = x → a lim g ( x ) f ( x ) W e kn o w f ( a ) an d g ( a ) b o t h e q u a l t o zero Q . E . D If f f f [ a , b ] [ a,\ b] [ a , b ] ( a , b ) ( a,\ b) ( a , b ) c ∈ ( a , b ) c\in ( a,\ b) c ∈ ( a , b ) Δ y Δ x = f ( b ) − f ( a ) b − a = f ′ ( c ) \displaystyle \frac{\Delta y}{\Delta x} =\frac{f( b) -f( a)}{b-a} =f^{\prime }( c) Δ x Δ y = b − a f ( b ) − f ( a ) = f ′ ( c )
f c o n t i n u o u s o v e r [ a , b ] ⟹ ∃ c , d ∈ [ a , b ] : f ( c ) ⩽ f ( x ) ⩽ f ( d ) f o r a l l x ∈ [ a , b ] f\ continuous\ over\ [ a,\ b] \Longrightarrow \exists \ c,\ d\in [ a,\ b] :f( c) \leqslant f( x) \leqslant f( d) \ for\ all\ x\in [ a,\ b] f co n t in u o u s o v er [ a , b ] ⟹ ∃ c , d ∈ [ a , b ] : f ( c ) ⩽ f ( x ) ⩽ f ( d ) f or a ll x ∈ [ a , b ]
critical points exists when non endpoint point at x = a { f ′ ( a ) = 0 f ′ ( a ) u n d e f i n e d x=a\ \begin{cases} f^{\prime }( a) =0\\ f^{\prime }( a) \ undefined \end{cases} x = a { f ′ ( a ) = 0 f ′ ( a ) u n d e f in e d
The definite integral of a continuous function f f f [ a , b ] [ a,\ b] [ a , b ] ∫ a b f ( x ) d x \displaystyle \int _{a}^{b} f( x) dx ∫ a b f ( x ) d x
∫ a b f ( x ) d x = lim n → ∞ ∑ i = 1 n f ( x i ) Δ x \displaystyle \int _{a}^{b} f( x) dx=\lim _{n\rightarrow \infty }\sum _{i=1}^{n} f( x_{i}) \Delta x ∫ a b f ( x ) d x = n → ∞ lim i = 1 ∑ n f ( x i ) Δ x Where Δ x = b − a n \displaystyle \Delta x=\frac{b-a}{n} Δ x = n b − a x i = a + Δ x ⋅ i x_{i} =a+\Delta x\cdot i x i = a + Δ x ⋅ i
Sum/Difference:
∫ a b [ f ( x ) ± g ( x ) ] d x = ∫ a b f ( x ) d x ± ∫ a b g ( x ) d x \displaystyle \int _{a}^{b}[ f( x) \pm g( x)] dx=\int _{a}^{b} f( x) dx\pm \int _{a}^{b} g( x) dx ∫ a b [ f ( x ) ± g ( x )] d x = ∫ a b f ( x ) d x ± ∫ a b g ( x ) d x
Constant multiple:
∫ a b k ⋅ f ( x ) d x = k ∫ a b f ( x ) d x \displaystyle \int _{a}^{b} k\cdot f( x) dx=k\int _{a}^{b} f( x) dx ∫ a b k ⋅ f ( x ) d x = k ∫ a b f ( x ) d x
Reverse interval:
∫ a b f ( x ) d x = − ∫ b a f ( x ) d x \displaystyle \int _{a}^{b} f( x) dx=-\int _{b}^{a} f( x) dx ∫ a b f ( x ) d x = − ∫ b a f ( x ) d x
Zero-length interval:
∫ a a f ( x ) d x = 0 \displaystyle \int _{a}^{a} f( x) dx=0 ∫ a a f ( x ) d x = 0
Adding intervals:
∫ a b f ( x ) d x + ∫ b c f ( x ) d x = ∫ a c f ( x ) d x \displaystyle \int _{a}^{b} f( x) dx+\int _{b}^{c} f( x) dx=\int _{a}^{c} f( x) dx ∫ a b f ( x ) d x + ∫ b c f ( x ) d x = ∫ a c f ( x ) d x
这么简单的东西相信你一定也知道怎么证。那证明就略略略了吧~
Let f f f [ a , b ] [ a,\ b] [ a , b ] F F F x x x [ a , b ] [ a,\ b] [ a , b ] F ( x ) = ∫ a x f ( t ) d t \displaystyle F( x) =\int _{a}^{x} f( t) dt F ( x ) = ∫ a x f ( t ) d t
Then F F F [ a , b ] [ a,\ b] [ a , b ] ( a , b ) ( a,\ b) ( a , b ) F ′ ( x ) = f ( x ) \displaystyle F^{\prime }( x) =f( x) F ′ ( x ) = f ( x ) x x x ( a , b ) ( a,\ b) ( a , b ) F F F f f f
Let f f f [ a , b ] [ a,\ b] [ a , b ] F F F [ a , b ] [ a,\ b] [ a , b ] f f f ( a , b ) ( a,\ b) ( a , b ) F ′ ( x ) = f ( x ) \displaystyle F^{\prime }( x) =f( x) F ′ ( x ) = f ( x )
If f f f [ a , b ] [ a,\ b] [ a , b ] ∫ a b f ( x ) d x = F ( b ) − F ( a ) \displaystyle \int _{a}^{b} f( x) dx=F( b) -F( a) ∫ a b f ( x ) d x = F ( b ) − F ( a )
∫ x n d x = x n + 1 n + 1 + C , n ≠ − 1 \displaystyle \int x^{n} dx=\frac{x^{n+1}}{n+1} +C,\ n\neq -1 ∫ x n d x = n + 1 x n + 1 + C , n = − 1
Yes that just simple!
Polynomials
∫ x n d x = x n + 1 n + 1 + C \displaystyle \int x^{n} dx=\frac{x^{n+1}}{n+1} +C ∫ x n d x = n + 1 x n + 1 + C
Radicals
∫ x n m d x = x n m + 1 n m + 1 + C \displaystyle \int \sqrt[m]{x^{n}} dx=\frac{x^{\frac{n}{m} +1}}{\frac{n}{m} +1} +C ∫ m x n d x = m n + 1 x m n + 1 + C
Trigonometric functions
∫ sin ( x ) d x = − cos ( x ) + C \displaystyle \int \sin( x) dx=-\cos( x) +C ∫ sin ( x ) d x = − cos ( x ) + C
∫ cos ( x ) d x = sin ( x ) + C \displaystyle \int \cos( x) dx=\sin( x) +C ∫ cos ( x ) d x = sin ( x ) + C
∫ sec 2 ( x ) d x = tan ( x ) + C \displaystyle \int \sec^{2}( x) dx=\tan( x) +C ∫ sec 2 ( x ) d x = tan ( x ) + C
∫ csc 2 ( x ) d x = − cot ( x ) + C \displaystyle \int \csc^{2}( x) dx=-\cot( x) +C ∫ csc 2 ( x ) d x = − cot ( x ) + C
∫ sec ( x ) tan ( x ) d x = sec ( x ) + C \displaystyle \int \sec( x)\tan( x) dx=\sec( x) +C ∫ sec ( x ) tan ( x ) d x = sec ( x ) + C
∫ csc ( x ) cot ( x ) d x = − csc ( x ) + C \displaystyle \int \csc( x)\cot( x) dx=-\csc( x) +C ∫ csc ( x ) cot ( x ) d x = − csc ( x ) + C
∫ sec x d x = ln ∣ sec x + tan x ∣ + C \displaystyle \int \sec xdx=\ln| \sec x+\tan x| +C ∫ sec x d x = ln ∣ sec x + tan x ∣ + C sec x + tan x \sec x+\tan x sec x + tan x
∫ csc x d x = ln ∣ csc x − cot x ∣ + C \displaystyle \int \csc xdx=\ln| \csc x-\cot x| +C ∫ csc x d x = ln ∣ csc x − cot x ∣ + C csc x − cot x \csc x-\cot x csc x − cot x
下面是另一种方法求这两个不定积分:
∫ sec x d x = ∫ 1 cos x d x = ∫ cos x cos 2 x d x = ∫ 1 1 − sin 2 x cos x d x L e t u = sin x = ∫ 1 ( 1 + u ) ( 1 − u ) d u = 1 2 ∫ ( 1 1 + u + 1 1 − u ) d u P a r t i a l f r a c t i o n s = 1 2 ln ∣ 1 + u 1 − u ∣ + C = 1 2 ln ∣ 1 + sin x 1 − sin x ∣ + C \begin{array}{ l l l } \displaystyle \int \sec xdx & =\displaystyle \int \frac{1}{\cos x} dx & \\ & =\displaystyle \int \frac{\cos x}{\cos^{2} x} dx & \\ & =\displaystyle \int \frac{1}{1-\sin^{2} x}\cos xdx & Let\ u=\sin x\\ & =\displaystyle \int \frac{1}{( 1+u)( 1-u)} du & \\ & =\displaystyle \frac{1}{2}\int \left(\frac{1}{1+u} +\frac{1}{1-u}\right) du & Partial\ fractions\\ & =\displaystyle \frac{1}{2}\ln\left| \frac{1+u}{1-u}\right| +C & \\ & =\displaystyle \frac{1}{2}\ln\left| \frac{1+\sin x}{1-\sin x}\right| +C & \end{array} ∫ sec x d x = ∫ cos x 1 d x = ∫ cos 2 x cos x d x = ∫ 1 − sin 2 x 1 cos x d x = ∫ ( 1 + u ) ( 1 − u ) 1 d u = 2 1 ∫ ( 1 + u 1 + 1 − u 1 ) d u = 2 1 ln 1 − u 1 + u + C = 2 1 ln 1 − sin x 1 + sin x + C L e t u = sin x P a r t ia l f r a c t i o n s
∫ csc x d x = ∫ 1 sin x d x = ∫ sin x sin 2 x d x = ∫ 1 1 − cos 2 x sin x d x L e t u = cos x = − ∫ 1 ( 1 + u ) ( 1 − u ) d u = − 1 2 ∫ ( 1 1 + u + 1 1 − u ) d u P a r t i a l f r a c t i o n s = − 1 2 ln ∣ 1 + u 1 − u ∣ + C = − 1 2 ln ∣ 1 + cos x 1 − cos x ∣ + C \begin{array}{ l l l } \displaystyle \int \csc xdx & =\displaystyle \int \frac{1}{\sin x} dx & \\ & =\displaystyle \int \frac{\sin x}{\sin^{2} x} dx & \\ & =\displaystyle \int \frac{1}{1-\cos^{2} x}\sin xdx & Let\ u=\cos x\\ & =\displaystyle -\int \frac{1}{( 1+u)( 1-u)} du & \\ & =\displaystyle -\frac{1}{2}\int \left(\frac{1}{1+u} +\frac{1}{1-u}\right) du & Partial\ fractions\\ & =\displaystyle -\frac{1}{2}\ln\left| \frac{1+u}{1-u}\right| +C & \\ & =\displaystyle -\frac{1}{2}\ln\left| \frac{1+\cos x}{1-\cos x}\right| +C & \end{array} ∫ csc x d x = ∫ sin x 1 d x = ∫ sin 2 x sin x d x = ∫ 1 − cos 2 x 1 sin x d x = − ∫ ( 1 + u ) ( 1 − u ) 1 d u = − 2 1 ∫ ( 1 + u 1 + 1 − u 1 ) d u = − 2 1 ln 1 − u 1 + u + C = − 2 1 ln 1 − cos x 1 + cos x + C L e t u = cos x P a r t ia l f r a c t i o n s
Exponential functions
∫ e x d x = e x + C \displaystyle \int e^{x} dx=e^{x} +C ∫ e x d x = e x + C
∫ a x d x = a x ln ( a ) + C \displaystyle \int a^{x} dx=\frac{a^{x}}{\ln( a)} +C ∫ a x d x = ln ( a ) a x + C
Logarithmic functions
∫ 1 x d x = ln ∣ x ∣ + C \displaystyle \int \frac{1}{x} dx=\ln |x|+C ∫ x 1 d x = ln ∣ x ∣ + C
Inverse trigonometric functions
∫ 1 a 2 − x 2 d x = arcsin ( x a ) + C \displaystyle \int \frac{1}{\sqrt{a^{2} -x^{2}}} dx=\arcsin\left(\frac{x}{a}\right) +C ∫ a 2 − x 2 1 d x = arcsin ( a x ) + C
∫ 1 a 2 + x 2 d x = 1 a arctan ( x a ) + C \displaystyle \int \frac{1}{a^{2} +x^{2}} dx=\frac{1}{a}\arctan\left(\frac{x}{a}\right) +C ∫ a 2 + x 2 1 d x = a 1 arctan ( a x ) + C
∫ u v d x = u ∫ v d x − ∫ ( u ′ ∫ v d x ) d x \displaystyle \int uvdx=u\int vdx-\int \left( u^{\prime }\int vdx\right) dx ∫ uv d x = u ∫ v d x − ∫ ( u ′ ∫ v d x ) d x
∫ sin n x d x = − 1 n sin n − 1 x cos x + n − 1 n ∫ sin n − 2 x d x \displaystyle \int \sin^{n} xdx=-\frac{1}{n}\sin^{n-1} x\cos x+\frac{n-1}{n}\int \sin^{n-2} xdx ∫ sin n x d x = − n 1 sin n − 1 x cos x + n n − 1 ∫ sin n − 2 x d x
∫ cos n x d x = 1 n cos n − 1 x sin x + n − 1 n ∫ cos n − 2 x d x \displaystyle \int \cos^{n} xdx=\frac{1}{n}\cos^{n-1} x\sin x+\frac{n-1}{n}\int \cos^{n-2} xdx ∫ cos n x d x = n 1 cos n − 1 x sin x + n n − 1 ∫ cos n − 2 x d x
∫ tan n x d x = 1 n − 1 tan n − 1 x − ∫ tan n − 2 x d x \displaystyle \int \tan^{n} xdx=\frac{1}{n-1}\tan^{n-1} x-\int \tan^{n-2} xdx ∫ tan n x d x = n − 1 1 tan n − 1 x − ∫ tan n − 2 x d x
∫ ( ln x ) n d x = x ( ln x ) n − n ∫ ( ln x ) n − 1 d x \displaystyle \int (\ln x)^{n} dx=x(\ln x)^{n} -n\int (\ln x)^{n-1} dx ∫ ( ln x ) n d x = x ( ln x ) n − n ∫ ( ln x ) n − 1 d x